⚡ Power in AC Circuits — Real, Reactive, and Apparent Power

🎯 Key Concept

In DC circuits, power is simple: voltage and current work together all the time.
In AC circuits, voltage and current may be out of phase, so power splits into three different forms.
Understanding these is essential for efficiency, billing, and real-world electrical design.

---

🔌 Why AC Power Is Different from DC Power

📚 Core Theory

In AC systems, reactive components (inductors and capacitors) store and release energy instead of consuming it.
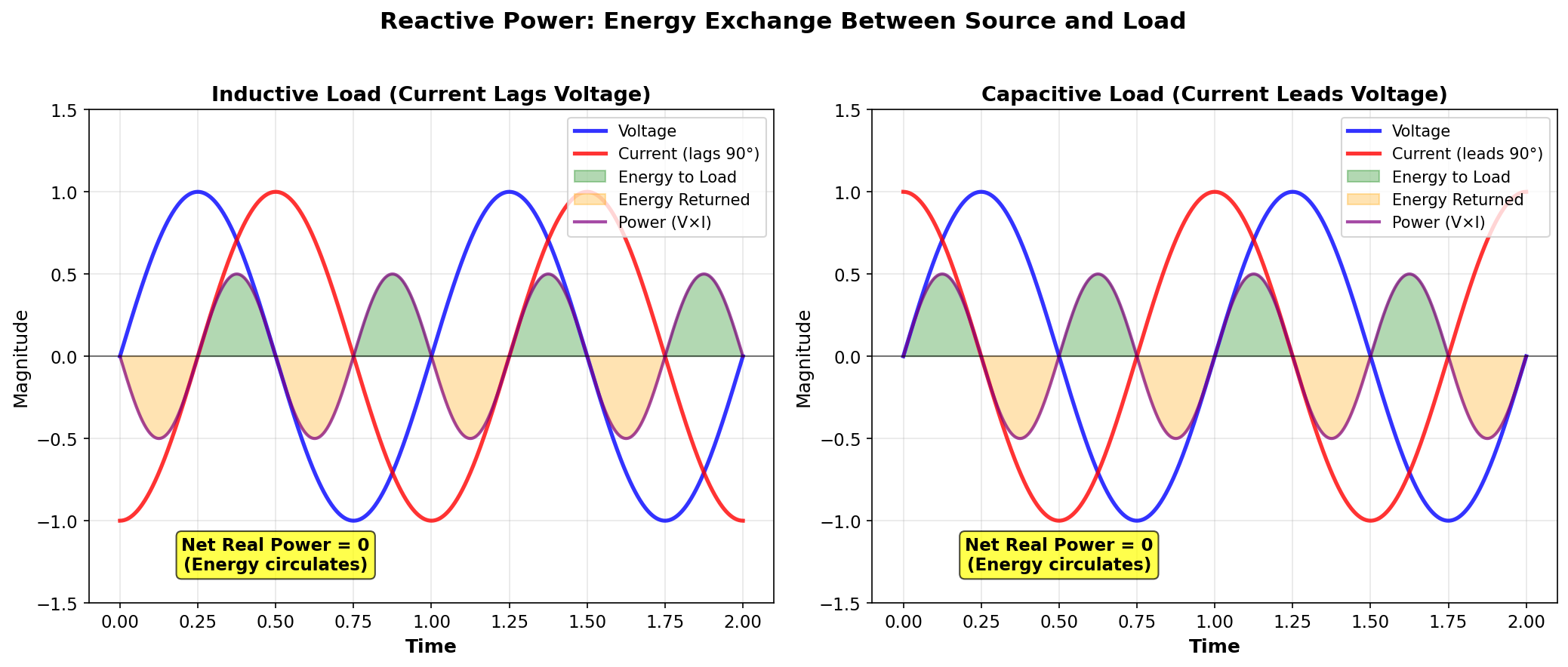
Because of this energy exchange, voltage and current are often out of phase by an angle $\theta$.

This phase difference changes how much power is actually useful versus how much is just circulating.

---

🔥 Real Power (P) — Useful Power

📚 Core Theory

Real Power is the power that performs actual work like:

• Lighting a bulb
• Running a motor
• Heating a resistor

Only resistive elements consume real power.

Unit: Watts (W)

Formula:

$$P = V \times I \times \cos(\theta)$$

Where:

• $V$ = RMS Voltage
• $I$ = RMS Current
• $\theta$ = Phase angle between voltage and current

⚡ Examples

Voltage (V)	Current (A)	Phase Angle	$\cos(\theta)$	Real Power (W)
10	1	$0^\circ$	1.0	10
10	1	$60^\circ$	0.5	5

Insight:
Even with the same voltage and current, real power drops when phase angle increases.

---

🔄 Reactive Power (Q) — Circulating Power

📚 Core Theory

Reactive Power represents energy that moves back and forth between:

• The source
• Capacitors and inductors

It does not perform useful work, but it:

• Increases current
• Causes copper losses
• Heats cables and transformers

Unit: Volt-Ampere Reactive (VAR)

Formula:

$$Q = V \times I \times \sin(\theta)$$

🚀 Key Insight

Reactive power:

• ❌ Does no useful work
• ❌ Increases losses
• ✅ Is reduced using power factor correction

---

📐 Apparent Power (S) — Total Power Seen

📚 Core Theory

Apparent Power is the product of voltage and current without considering phase angle.

Unit: Volt-Amperes (VA)

Formula:

$$S = V \times I$$

It represents the total load on generators, transformers, and cables.

⚡ Example

Voltage (V)	Current (A)	Apparent Power (VA)
10	1	10

But real power may be much lower depending on $\theta$.

---

📊 The Power Triangle

📚 Core Theory

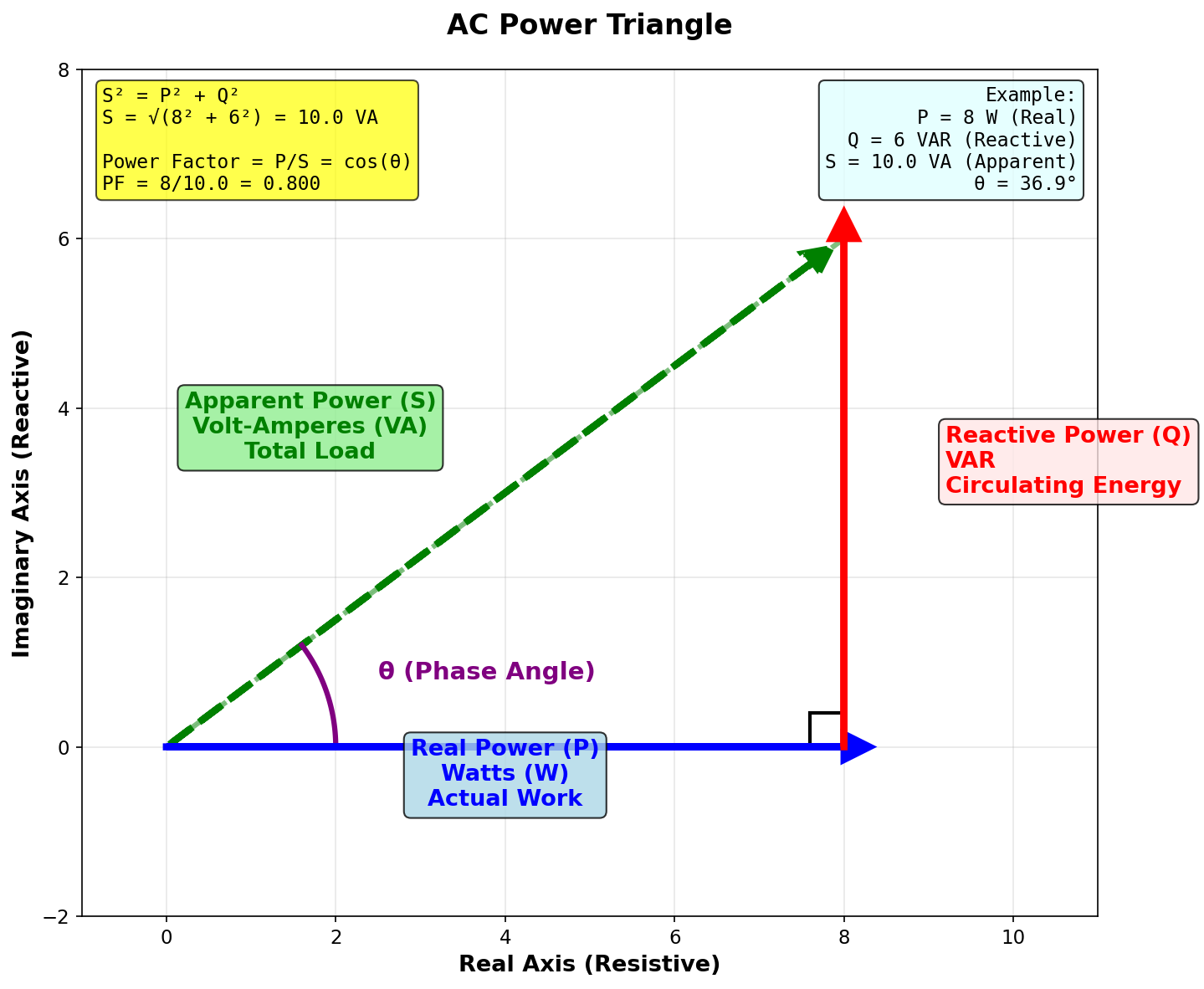
The relationship between the three powers is:

$$S^2 = P^2 + Q^2$$

• Horizontal: Real Power (P)
• Vertical: Reactive Power (Q)
• Hypotenuse: Apparent Power (S)
• Angle: Phase angle $\theta$

---

⚙️ Power Factor — Efficiency Indicator

📚 Core Theory

Power Factor (PF) tells how efficiently power is being used.

Formula:

$$\text{Power Factor} = \frac{P}{S} = \cos(\theta)$$

• PF = 1 → Perfect (purely resistive)
• PF ≈ 0 → Very inefficient (highly reactive)

⚡ Power Factor Comparison

Load Type	Phase Angle	Power Factor
Heater	$0^\circ$	1.0
Motor (no correction)	$60^\circ$	0.5
Motor (corrected)	$20^\circ$	0.94

---

🏭 Real-World Impact

📚 Core Theory

• Your electricity bill charges for real power (W)
• Transmission lines carry apparent power (VA)
• Reactive power wastes infrastructure capacity

This is why industries install capacitor banks to improve power factor and reduce penalties.

---

🚀 Key Takeaway

🚀 Key Takeaway

• AC power splits into Real (P), Reactive (Q), and Apparent (S)
• Phase angle is the reason AC power is complex
• Power factor correction saves money, energy, and equipment life
• Always size cables, transformers, and generators using VA, not W alone

Final Insight:
⚡ AC power isn’t just about volts and amps — phase angle changes everything.