Kirchhoff's Current and Voltage Laws (KCL, KVL)

The Foundation for Circuit Analysis

These two laws are the foundation for circuit analysis. They help you solve circuits with multiple loops and junctions where simple Ohm's Law isn't enough.

Why These Laws Matter

Kirchhoff's Laws are conservation principles:

• KCL - Current is conserved (what goes in must come out)
• KVL - Energy is conserved (what goes up must come down)

Together, they let you analyze any circuit, no matter how complex!

---

🌊 Kirchhoff's Current Law (KCL)

The Law

KCL Statement

"The total current flowing into a node must equal the total current flowing out."

In other words: Current is conserved. No current mysteriously disappears or appears.

A node (or junction) is any point where two or more wires connect.

Understanding KCL

Think of a highway intersection:

• Cars entering the intersection = current flowing in
• Cars leaving the intersection = current flowing out
• No cars disappear or appear inside the intersection
• Cars in = Cars out

Same principle applies to electrical current!

The Mathematical Expression

$$Σ I_in = Σ I_out$$

Or equivalently:

$$Σ I = 0$$

Where currents flowing into the node are positive, and currents flowing out are negative.

---

KCL Example

Practical Example

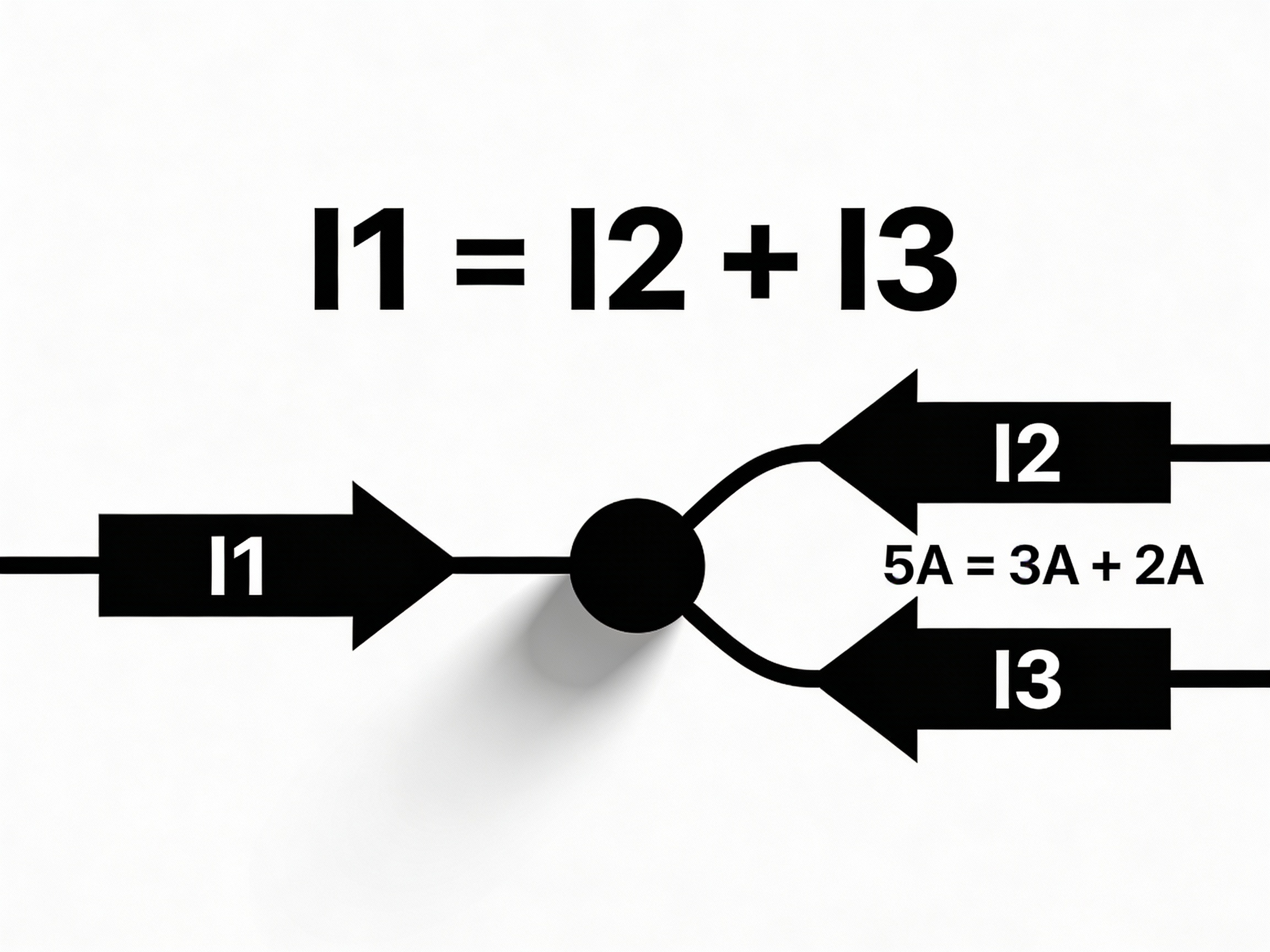
At a node where 3 wires meet:

Given:

• 5A flows in from the left
• 2A flows out the top

Question: How much current flows out to the right?

Solution:

Current IN = Current OUT
5A = 2A + I_right
I_right = 5A - 2A
I_right = 3A

Answer: 3A must flow out to the right!

Multiple Current Example

Wire	Direction	Current
Wire 1	IN	10A
Wire 2	OUT	4A
Wire 3	OUT	3A
Wire 4	OUT	?

10A (in) = 4A + 3A + I4 (out)
I4 = 10A - 7A = 3A

---

⚡ Kirchhoff's Voltage Law (KVL)

The Law

KVL Statement

"The sum of all voltages around a closed loop equals zero."

In other words: What goes up must come down. If you gain voltage from a battery, you must lose it through resistors.

Energy is conserved - you can't create or destroy voltage in a loop!

Understanding KVL

Think of hiking around a mountain loop:

• You climb up (gain altitude) = battery provides voltage
• You walk down (lose altitude) = resistors drop voltage
• When you return to start = net altitude change is zero

Same principle applies to voltage in a circuit loop!

The Mathematical Expression

$$Σ V = 0$$

Where:

• Voltage rises (batteries) are positive
• Voltage drops (resistors) are negative

---

KVL Example

Practical Example

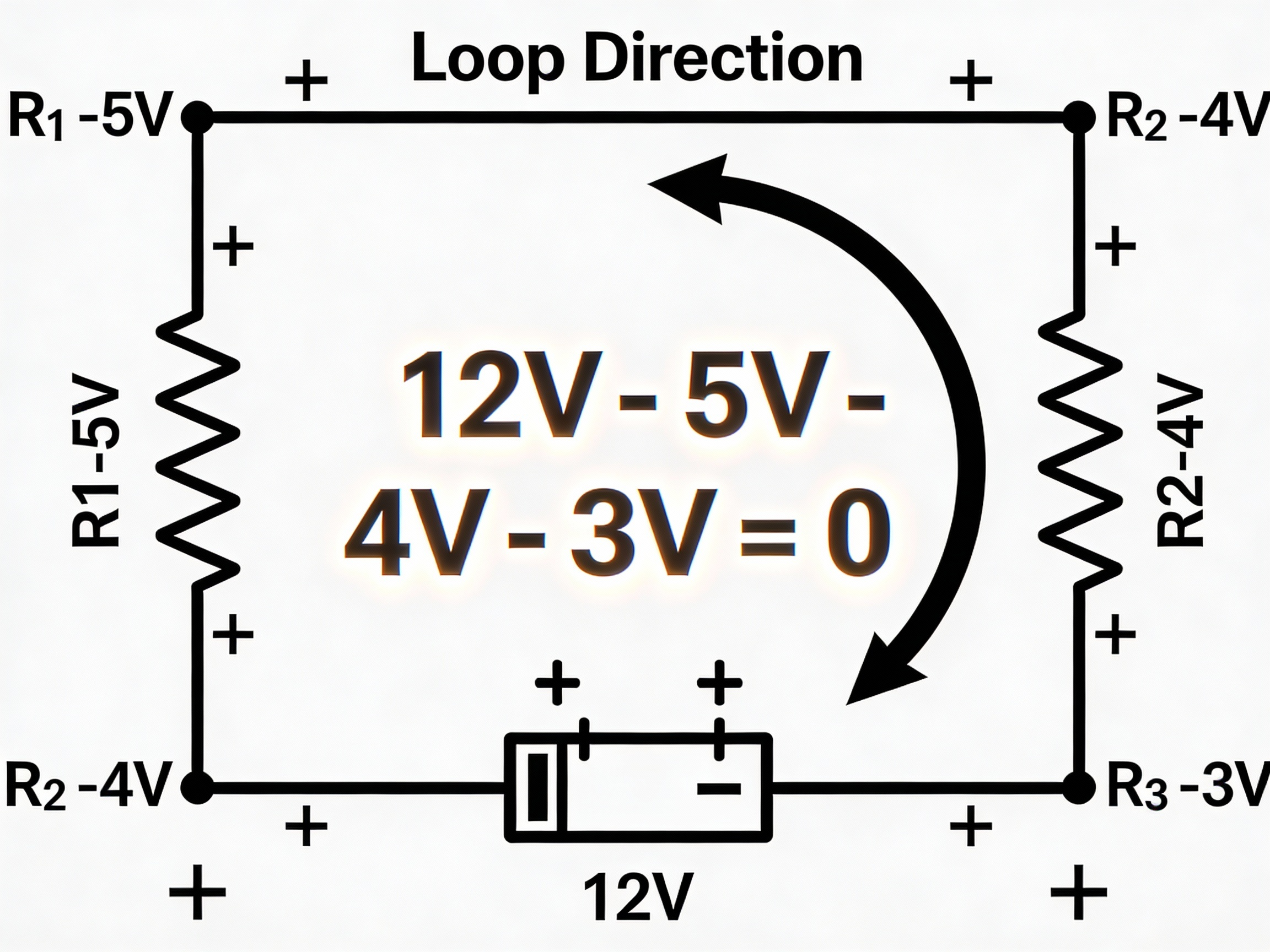
In a loop with:

Given:

• +12V battery (voltage gain)
• -5V across resistor 1 (voltage loss)
• -4V across resistor 2 (voltage loss)
• -3V across resistor 3 (voltage loss)

Checking KVL:

Sum of all voltages = 0
+12V - 5V - 4V - 3V = 0
12V - 12V = 0 ✓

Result: The law is satisfied! Energy is conserved.

Finding Unknown Voltage

Component	Voltage	Type
Battery	+9V	Rise
Resistor 1	-3V	Drop
Resistor 2	-2V	Drop
Resistor 3	?	Drop

+9V - 3V - 2V - V3 = 0
V3 = 9V - 3V - 2V
V3 = 4V

---

🔧 Applying Kirchhoff's Laws Together

Most real circuits require both laws working together:

Combined Analysis

KCL handles current distribution at nodes

KVL handles voltage distribution around loops

Together they create a system of equations you can solve!

Step-by-Step Circuit Analysis

1. Identify all nodes → Apply KCL at each node
2. Identify all loops → Apply KVL around each loop
3. Create equations → One equation per node/loop
4. Solve simultaneously → Find unknown currents and voltages

---

💡 Why These Laws Matter

Foundation for Everything

Kirchhoff's Laws enable you to:

• ✅ Analyze multi-loop circuits (solar panels in series-parallel)
• ✅ Find unknown currents in complex networks
• ✅ Validate circuit designs before building
• ✅ Troubleshoot faulty circuits by checking conservation
• ✅ Foundation for advanced techniques:
  • Mesh analysis
  • Nodal analysis
  • Thevenin/Norton theorems

Real-World Applications

Application	Which Law	Why
Power distribution	KCL	Current splits at junctions
Battery bank analysis	KVL	Voltages add in series
LED array design	Both	Current distribution + voltage drops
Solar panel arrays	Both	Series-parallel combinations
Complex PCB circuits	Both	Multiple paths and loops

---

📊 Quick Reference Summary

KCL (Current Law)

Property	Description
Applies to	Nodes (junctions)
Conservation of	Current (charge)
Formula	Σ I_in = Σ I_out
Key idea	Current in = Current out
Analogy	Cars at intersection

KVL (Voltage Law)

Property	Description
Applies to	Closed loops
Conservation of	Energy (voltage)
Formula	Σ V = 0
Key idea	Voltage rises = Voltage drops
Analogy	Hiking around mountain

---

🎯 Practice Tips

Mastering Kirchhoff's Laws

For KCL:

1. Pick a direction convention (in = positive, out = negative)
2. Label all currents at the node
3. Write equation: sum of all currents = 0
4. Solve for unknown

For KVL:

1. Pick a loop direction (clockwise or counterclockwise)
2. Walk around the loop, noting voltage rises (+) and drops (-)
3. Write equation: sum of all voltages = 0
4. Solve for unknown

Pro tip: Draw arrows on your circuit diagram to show current direction and loop direction!

Common Mistakes to Avoid

Common Errors

❌ Forgetting signs - Pay attention to + and - directions

❌ Missing currents - Count all wires at a node

❌ Incomplete loops - Make sure loop returns to starting point

❌ Mixing up laws - KCL for nodes, KVL for loops

✅ Always check: Do currents balance? Do voltages sum to zero?

---

🚀 Advanced Applications

These laws form the basis for:

Technique	Uses KCL/KVL	Purpose
Mesh Analysis	KVL	Systematic loop analysis
Nodal Analysis	KCL	Systematic node analysis
Superposition	Both	Multiple source analysis
Thevenin/Norton	Both	Circuit simplification
Circuit simulation	Both	Computer-aided analysis

---

Remember

Kirchhoff's Laws are fundamental conservation principles:

KCL - Current Conservation:

• 🌊 Applies at nodes (junctions)
• Current in = Current out
• No current appears or disappears
• Formula: Σ I = 0

KVL - Voltage Conservation:

• ⚡ Applies around closed loops
• Voltage rises = Voltage drops
• Energy is conserved
• Formula: Σ V = 0

Together they solve any circuit:

• Start with what you know
• Apply the appropriate law
• Create and solve equations
• Verify your results

These laws never fail - if your calculations don't work, check your assumptions and signs!