Capacitance and Inductance — How Electricity Learns Time
Why Resistance Alone Is Not Enough
Up to this point, we have been thinking of electrical circuits as if they react instantly. We apply a voltage, and current starts flowing immediately, exactly as predicted by Ohm's Law. For simple circuits that contain only resistors, this assumption works reasonably well.
However, real electrical and electronic systems do not behave so simply.
In the real world, circuits have a kind of memory. They do not like sudden changes. When voltage or current is applied abruptly, some components oppose that change. Instead of responding instantly, they take time.
This time-dependent behavior cannot be explained using resistance alone.
The reason is that some components are able to store energy temporarily and release it later. Because of this energy storage, the present behavior of the circuit depends not only on what is happening now, but also on what happened just before.
To understand how circuits behave over time, we need to introduce two important concepts: capacitance and inductance.
🔧 Symbols and Units
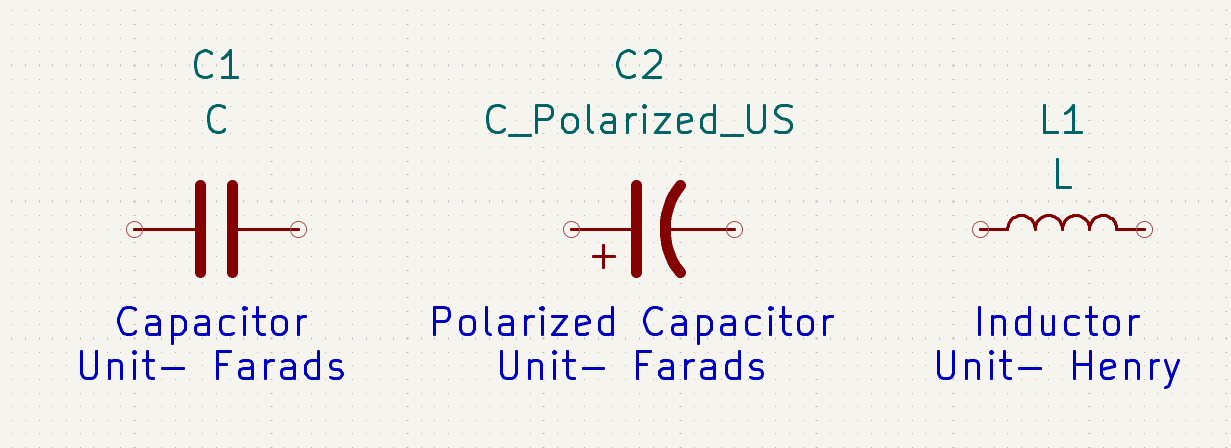
| Component | Symbol | Unit | What it stores |
|---|---|---|---|
| Capacitor | || (two parallel plates) | Farads (F) | Electric charge/energy |
| Inductor | Coil symbol | Henry (H) | Magnetic energy |
🌊 Understanding Time Delays with Analogies
The Water Tank Analogy
A useful way to visualize this is with a water analogy.
Imagine water flowing through a pipe. If you open a valve, water starts flowing immediately at the other end. This is similar to a purely resistive circuit, where current responds instantly to voltage.
Now suppose you insert a water tank in the middle of the pipe. When you open the valve, water first begins to fill the tank. Only after the tank starts filling up does water begin to come out from the other side.
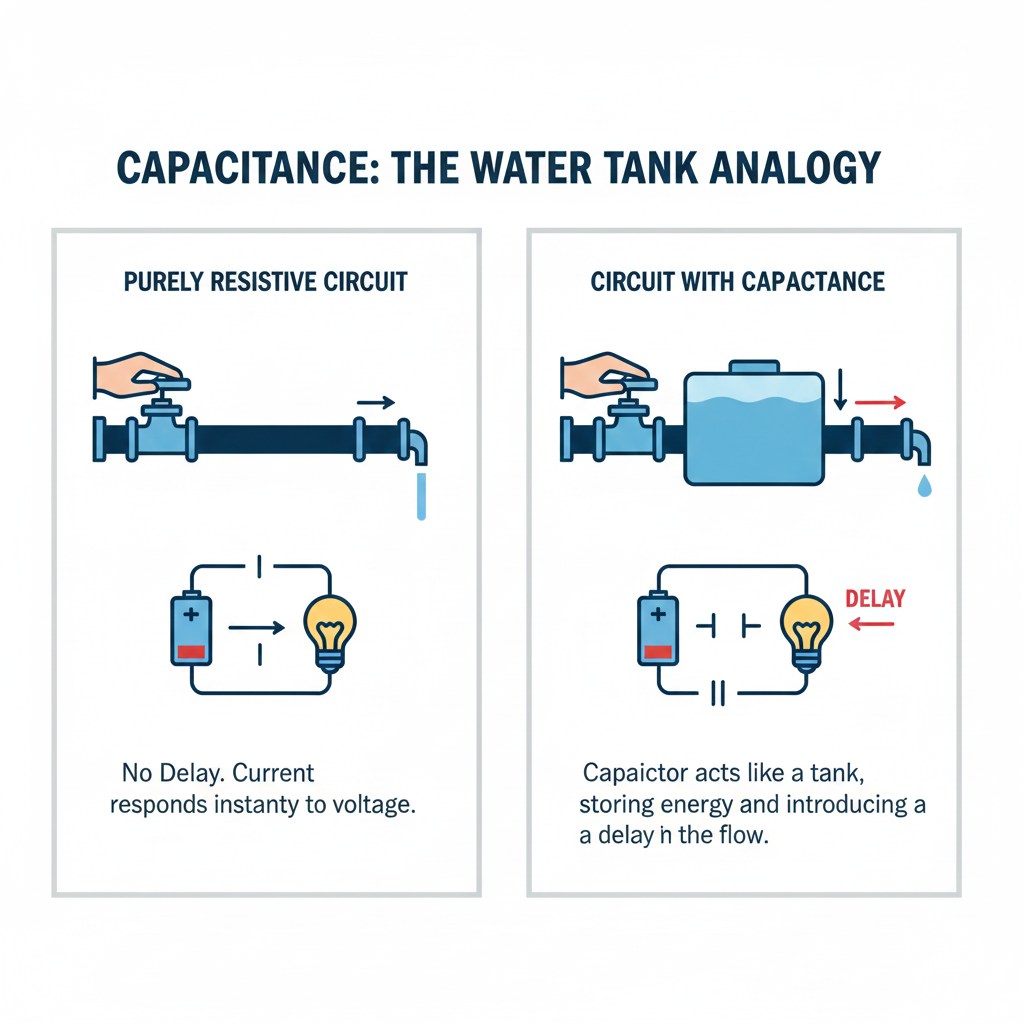The tank introduces a delay in the flow.
Capacitance in an electrical circuit behaves in a similar way. It stores energy temporarily and delays the response of voltage or current, depending on how the circuit is arranged.
The Spring and Ball Analogy
Another helpful analogy is a spring with a ball attached. If you release the ball, it does not instantly reach its final position. The spring stretches gradually, stores energy, and only after some time does the system settle.
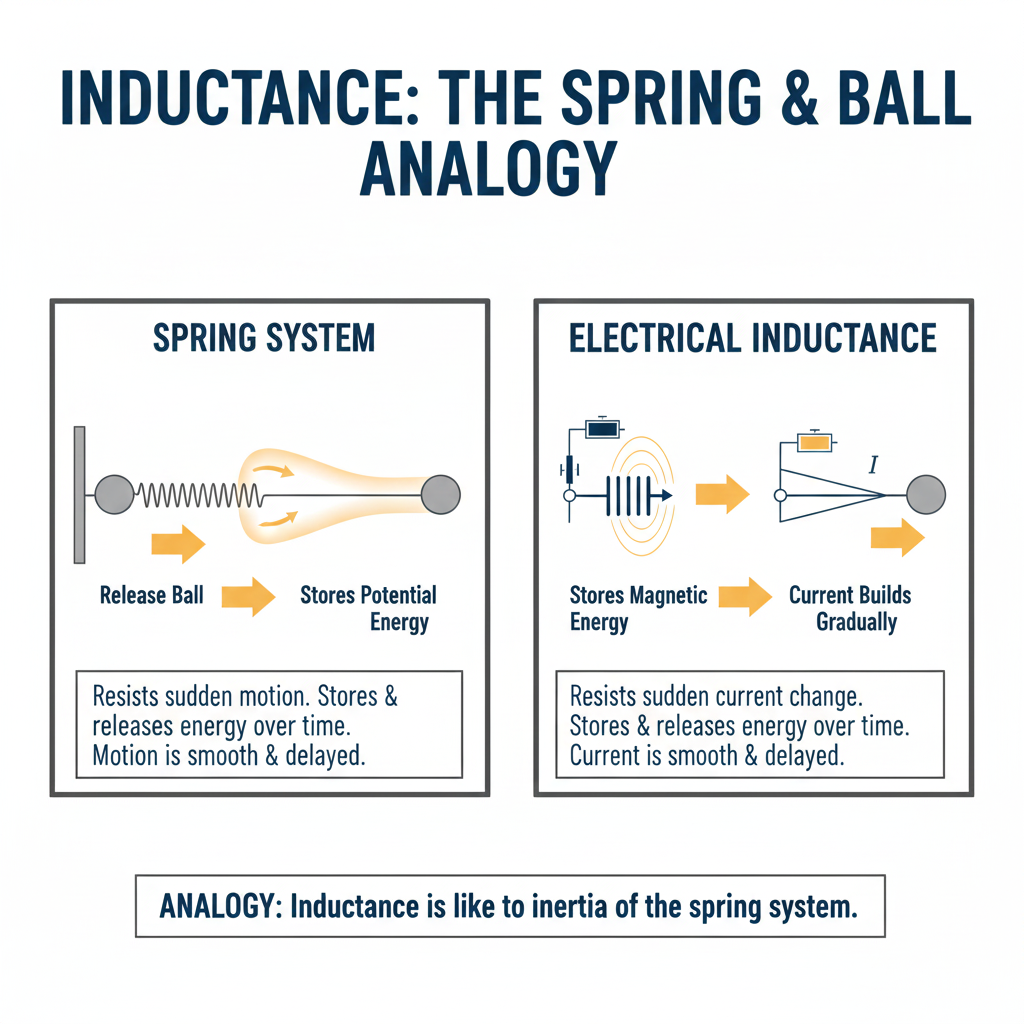The motion is smooth and delayed, not instantaneous.
Inductance behaves in a similar manner in electrical systems. It resists sudden changes in current, stores energy in a magnetic field, and releases it gradually over time.
In electronic systems, capacitors and inductors are deliberately used wherever:
- ⏱️ Timing circuits are needed
- 🌊 Smoothing voltage/current fluctuations
- 📡 Filtering signals
- 🔋 Temporary energy storage
They are the reason circuits can delay signals, shape waveforms, and behave differently over time instead of responding instantly.
⚡ Capacitance — Storing Energy in an Electric Field
Capacitance is the ability of a system to store electric charge.
A capacitor consists of two conductive plates separated by an insulating material called a dielectric. When a voltage is applied across these plates, electrons do not jump directly from one plate to the other. Instead, they accumulate on one plate and are removed from the other, creating an electric field between them.
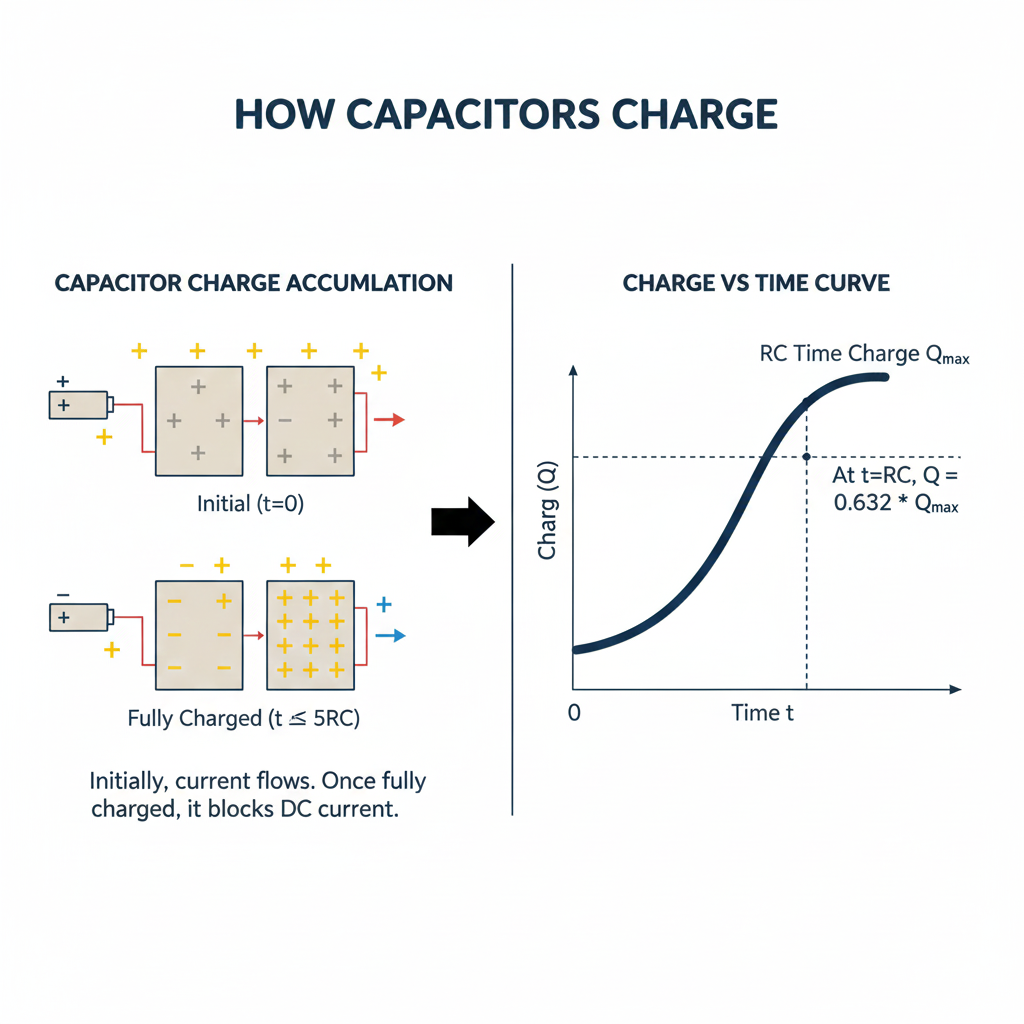
How Capacitors Charge
As the capacitor charges:
- Current flows initially (when voltage is first applied)
- As the voltage across the capacitor approaches the applied voltage, the charging current gradually reduces
- Once fully charged, the capacitor blocks further DC current, behaving like an open circuit
This means a capacitor:
- ✅ Allows current to flow only while voltage is changing
- ❌ Blocks steady DC
- 🔋 Stores energy temporarily
This property makes capacitors essential for filtering, smoothing power supplies, timing circuits, and signal coupling.
Capacitance Units
Capacitance is measured in farads (F), but practical values are usually:
- Microfarads (µF) = 10⁻⁶ F
- Nanofarads (nF) = 10⁻⁹ F
- Picofarads (pF) = 10⁻¹² F
| Capacitor Type | Typical Value | Common Use |
|---|---|---|
| Electrolytic | 1µF - 10,000µF | Power supply filtering |
| Ceramic | 10pF - 1µF | Signal coupling, bypass |
| Film | 1nF - 10µF | Audio circuits, timing |
🔄 Voltage-Current Behavior of a Capacitor
Unlike a resistor, a capacitor does not follow Ohm's Law directly. The current through a capacitor depends on how fast the voltage changes, not on the voltage value itself.
- If voltage changes rapidly → large current flows
- If voltage is constant → current becomes zero
This is why capacitors:
- ✅ Pass AC signals (voltage constantly changing)
- ❌ Block DC signals (voltage constant)
- 🌊 Smooth voltage variations (resist sudden changes)
In simple terms: A capacitor resists sudden changes in voltage.
🧲 Inductance — Storing Energy in a Magnetic Field
Inductance is the ability of a conductor to store energy in a magnetic field when current flows through it.
An inductor is typically made by winding a wire into a coil. When current flows through the coil, a magnetic field forms around it.
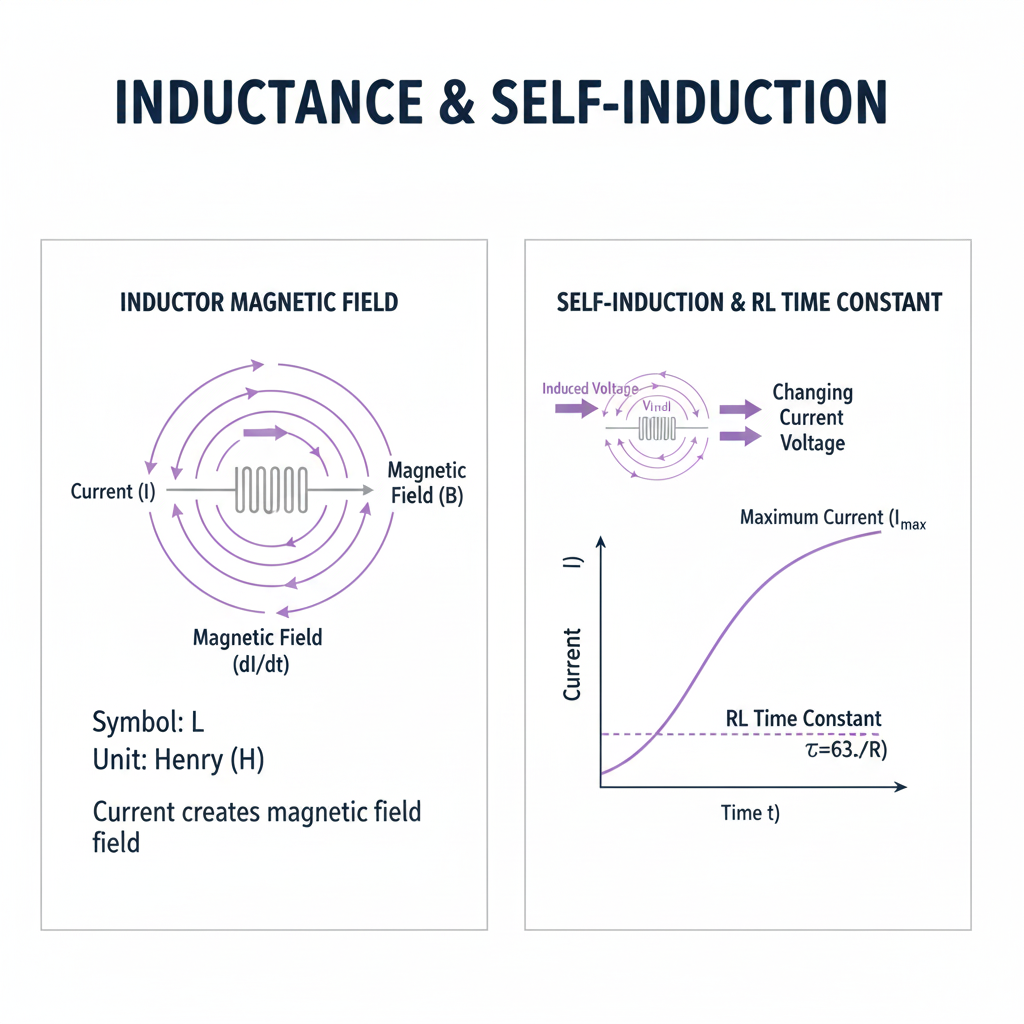
Self-Induction
If the current tries to change suddenly, the magnetic field opposes this change by inducing a voltage in the opposite direction. This phenomenon is known as self-induction.
An inductor therefore:
- ✅ Allows DC current to flow freely (once established)
- ❌ Opposes sudden changes in current
- 🧲 Stores energy in a magnetic field
Inductance is measured in henries (H), with practical values in:
- Millihenries (mH) = 10⁻³ H
- Microhenries (µH) = 10⁻⁶ H
| Inductor Type | Typical Value | Common Use |
|---|---|---|
| Power inductors | 1µH - 1mH | Switching power supplies |
| RF chokes | 1µH - 100µH | Radio frequency circuits |
| Transformers | 1mH - 10H | AC power conversion |
🔄 Voltage-Current Behavior of an Inductor
Unlike a resistor or capacitor, an inductor reacts to changes in current.
When current starts to increase, the inductor initially resists it.
When current tries to decrease, the inductor resists that too.
This means:
- 🌊 Current through an inductor changes gradually
- ⚡ Voltage appears across the inductor only when current changes
In simple terms: An inductor resists sudden changes in current.
📊 Key Insight - Understanding the Differences
This single table, once understood, removes confusion forever:
| Component | Resists change in | Stores energy in | Response to DC |
|---|---|---|---|
| Resistor | Nothing (instant response) | No storage | Constant current flows |
| Capacitor | Voltage | Electric field | Blocks (open circuit) |
| Inductor | Current | Magnetic field | Passes freely (short circuit) |
Comparison Table
| Property | Resistor | Capacitor | Inductor |
|---|---|---|---|
| Primary function | Limit current | Store charge | Store magnetic energy |
| Opposes changes in | Nothing | Voltage | Current |
| Energy storage | None (dissipates as heat) | Electric field | Magnetic field |
| DC behavior | Allows current | Blocks after charging | Allows current |
| AC behavior | Same as DC | Passes (acts as conductor) | Opposes (acts as resistor) |
| Unit | Ohms (Ω) | Farads (F) | Henry (H) |
💡 Why Capacitors and Inductors Matter in Electronics
Understanding these components explains:
- 🔌 Why power supplies ripple - Capacitors smooth out voltage fluctuations
- 🏭 Why motors draw high starting current - Inductance resists sudden current changes
- 📡 Why signals distort or smooth out - Capacitance and inductance filter frequencies
- 🎵 Why filters and oscillators work - LC circuits create resonance
- ⚡ Why switching power supplies exist - Inductors transfer energy efficiently
Common Applications
| Application | Component Used | Why? |
|---|---|---|
| Power supply smoothing | Capacitor | Fills in voltage dips |
| Motor starting | Inductor | Controls current surge |
| Audio crossover | Capacitor + Inductor | Frequency filtering |
| RF tuning | Capacitor + Inductor | Resonant circuits |
| Timing circuits | Capacitor + Resistor | RC time constant |
| Energy storage | Capacitor or Inductor | Temporary power reserve |
🚀 The Path Forward
Without understanding capacitors and inductors, advanced topics become guesswork:
- ❌ Diodes and transistors
- ❌ Switch-mode power supplies (SMPS)
- ❌ Op-amp circuits
- ❌ Microcontroller power design
- ❌ Signal processing
- ❌ RF and wireless circuits
Master these fundamentals now to build a solid foundation for everything that follows!
Capacitors and inductors bring the dimension of TIME into electrical circuits.
- ⚡ Resistors respond instantly
- 🔋 Capacitors resist voltage changes
- 🧲 Inductors resist current changes
Together, these three components form the foundation of all circuit behavior, from simple filters to complex power electronics and communication systems.