Phase Angle and Phasor Diagrams – Visualizing AC Relationships

In AC circuits, resistance and reactance do not add like ordinary numbers because they are out of phase.
To understand this visually, we use phasor diagrams.

note

Phasor diagrams turn time-based sine waves into static vectors, making AC analysis much simpler.

---

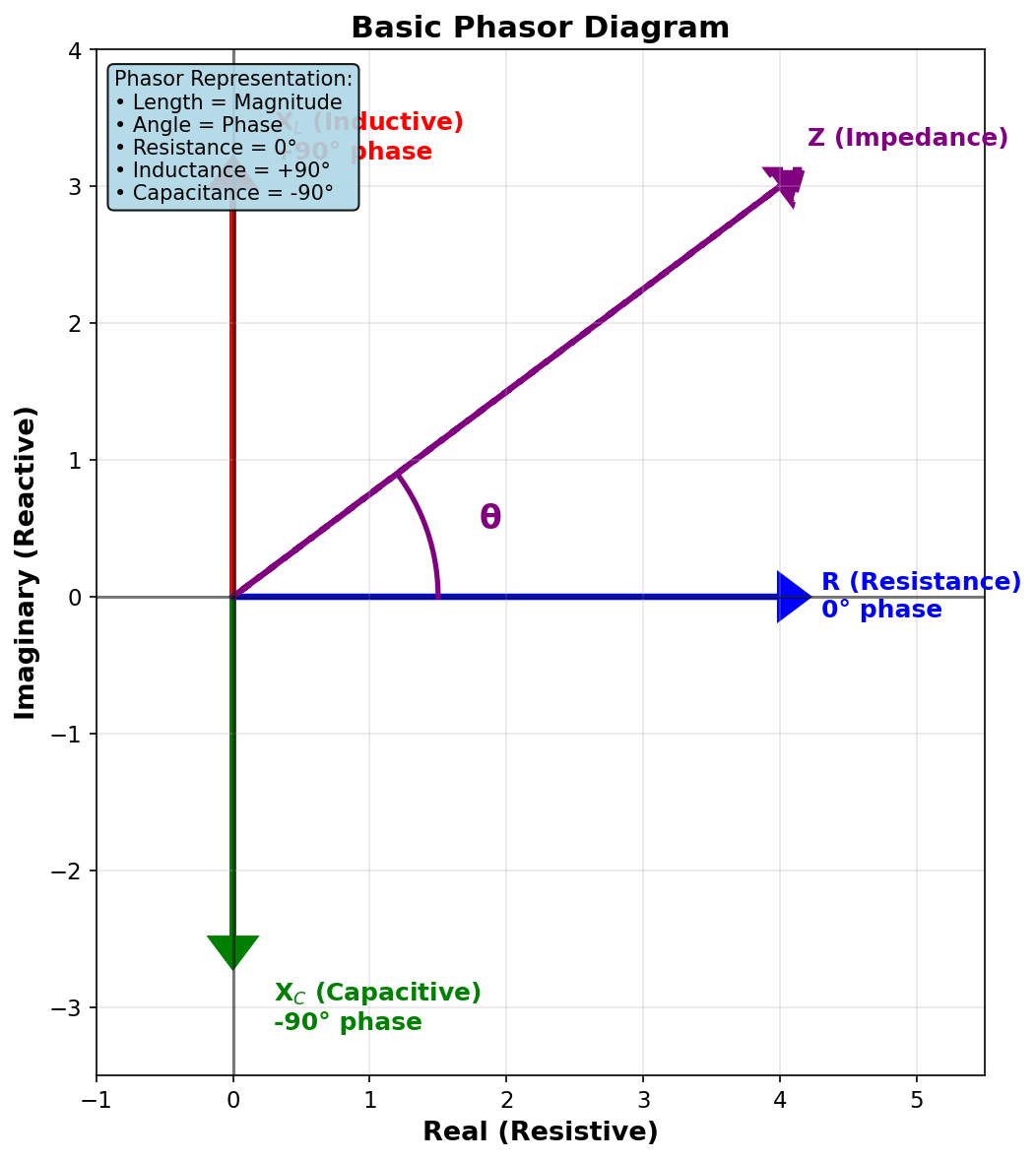
What Is a Phasor?

A phasor is a rotating vector that represents a sinusoidal voltage or current.

• Length of the arrow → magnitude (voltage or current)
• Angle of the arrow → phase relative to a reference

Think of a clock hand:

• Length = how strong the signal is
• Angle = where the signal is in its cycle

---

Phase Angle

The phase angle is the time difference between voltage and current, expressed as an angle.

Measured in:

• Degrees (0°–360°)
• Radians (0–2π)

Phase Relationships

important

Different components create different phase shifts.

Circuit Type	Phase Relationship
Pure resistive	Voltage and current in phase (0°)
Pure inductive	Current lags voltage by 90°
Pure capacitive	Current leads voltage by 90°

---

Why Phase Angle Matters

important

Phase angle determines how efficiently a circuit uses power.

It affects:

• Power factor
• Reactive power (stored energy)
• Real power (useful work)
• Resonance conditions

---

Phasor Diagram Construction

To draw a phasor diagram:

1. Draw a horizontal reference line (usually resistance)
2. Draw reactance at ±90°:
   • Upward for inductive
   • Downward for capacitive
3. Draw the diagonal vector combining both
4. The angle between impedance and resistance is the phase angle

---

Example: RL Circuit

Given:

• Resistance = 100 Ω
• Inductive reactance = 80 Ω

Phasors:

• R → horizontal (0°)
• XL → vertical up (90°)
• Z → diagonal

Phase angle:

$$\theta = \tan^{-1}\left(\frac{X_L}{R}\right) \approx 39^\circ$$

note

A 39° phase angle means current lags voltage by 39°.

---

Real-World Impact

warning

Poor phase angle means wasted power.

In power systems:

• Large phase angles cause low power factor
• Utilities charge penalties for excessive reactive power
• Capacitor banks are used to correct phase angle

---

Why Phasors Are Powerful

tip

Phasors convert trigonometry into simple geometry.

• Time-domain sine waves → vectors
• Differential equations → algebra
• Complex AC behavior → right triangles

---

Key Takeaway

important

Phasor diagrams are the bridge between intuition and calculation.

They make phase angle, impedance, and power relationships visible — and without them, AC circuit analysis would be nearly impossible.