Skip to main content

🧠 Combinational and Sequential Circuits: Building Complexity from Simple Gates

Logic gates by themselves are simple. But when we combine them in structured ways, we get powerful systems that can calculate, remember, and make decisions over time.
These systems fall into two big categories:

  • Combinational Circuits → No memory
  • Sequential Circuits → With memory

This distinction is one of the most important ideas in digital electronics.

🔷 Combinational Circuits​

What Are Combinational Circuits?​

A combinational circuit produces an output that depends only on the current inputs.

There is:

  • ❌ No memory
  • ❌ No storage
  • ❌ No history

Mathematically:

Output=f(Current Inputs)\text{Output} = f(\text{Current Inputs})

If the inputs change, the output changes immediately (after a small propagation delay).

🧮 Examples of Combinational Circuits​

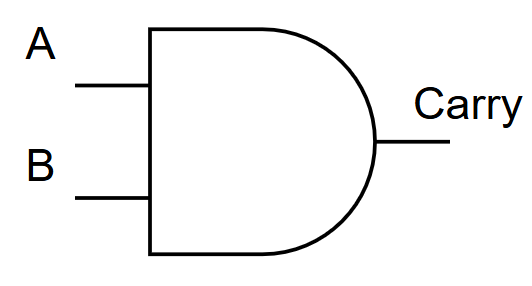
1️⃣ Adders​

  • Half Adder
  • Full Adder
  • Binary adders inside CPUs

Example:

Sum=A⊕B\text{Sum} = A \oplus B

Carry=A⋅B\text{Carry} = A \cdot B

2️⃣ Multiplexers (MUX)​

A multiplexer selects one input out of many based on select lines.

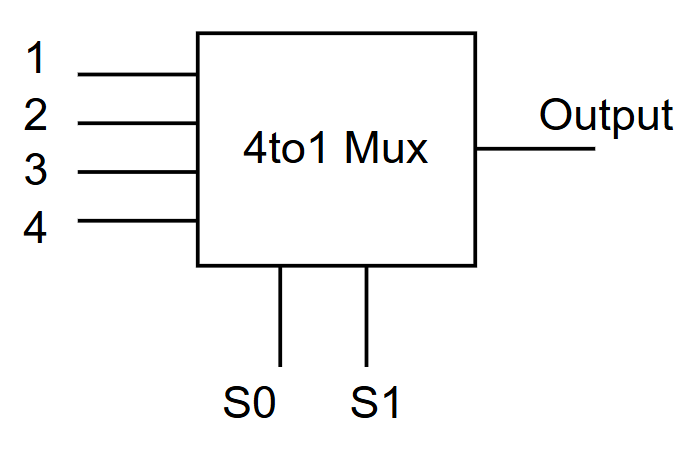Remember:

Multiplexer is many to one Demultiplexer is one to many (vice versa of MUX)

Example:

  • Choose one sensor from 8
  • Select which data goes to the CPU

3️⃣ Decoders & Encoders​

  • Decoder: Binary input → one active output

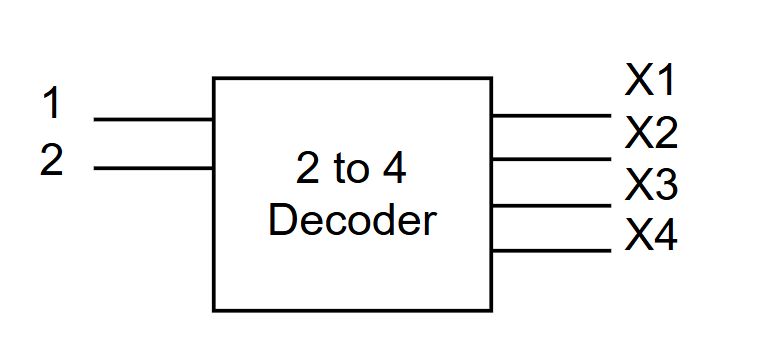
  • Encoder: One active input → binary output
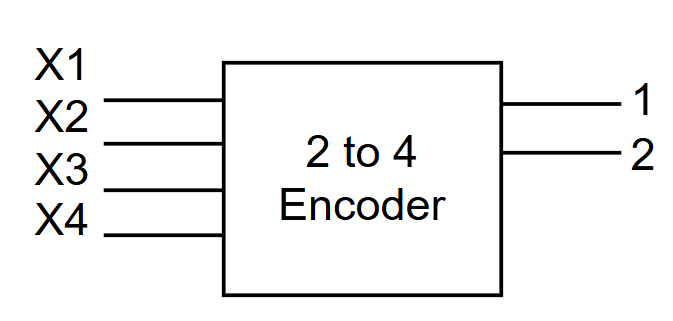    Used in:

  • Keyboards

  • Address decoding

  • Memory selection

4️⃣ Comparators​

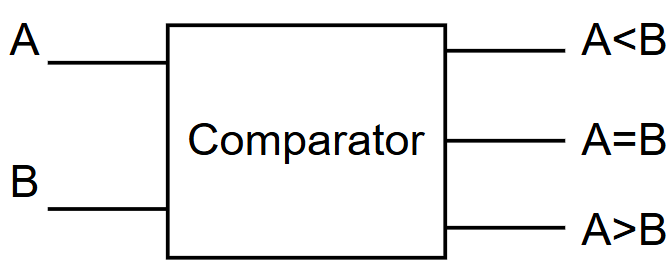
Compare two numbers:

  • Greater than
  • Less than
  • Equal to

Used in:

  • ALUs
  • Control logic
  • Decision circuits

🔑 Key Property of Combinational Circuits​

Same input → same output
Always
No exceptions
Instant output

They cannot remember anything.

🔶 Sequential Circuits​

What Are Sequential Circuits?​

Example Register Sequential circuits do have memory.

Their output depends on:

  • Current inputs
  • Previous state (history)

Mathematically:

Output=f(Current Inputs,Previous State)\text{Output} = f(\text{Current Inputs}, \text{Previous State})

This is what allows electronics to remember, count, and sequence actions.

🧠 Why Memory Is Needed​

Without memory:

  • You can add numbers
  • But you can’t remember results
  • You can’t count
  • You can’t run programs

Memory turns logic into computation.

🔁 The Building Block of Memory: Flip-Flops​

A flip-flop stores exactly one bit:

  • 0 or 1

It remembers this value until told to change.

Common Flip-Flop Types​

1️⃣ SR Flip-Flop​

  • Set / Reset
  • Simple but has illegal states [[sr-latch-nand-circuit.svg]]

2️⃣ D Flip-Flop (MOST IMPORTANT)​

  • Stores the value of D on a clock edge
  • Output stays constant until next clock

Rule:

Qnext=DQ_{\text{next}} = D

This is the backbone of:

  • Registers
  • Memory
  • CPUs

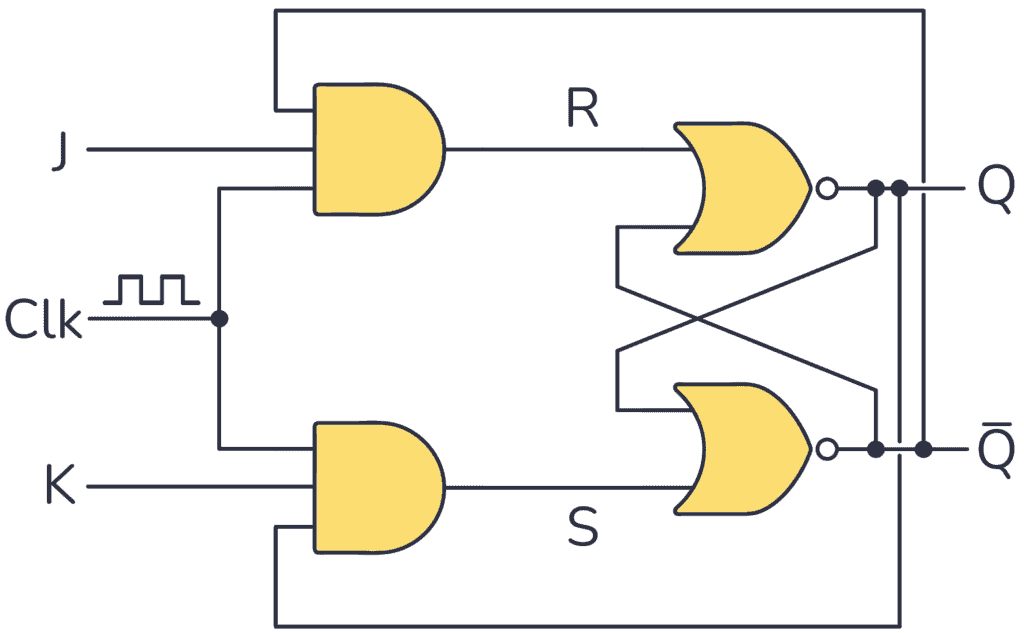
3️⃣ JK Flip-Flop​

  • Improved SR
  • Can toggle

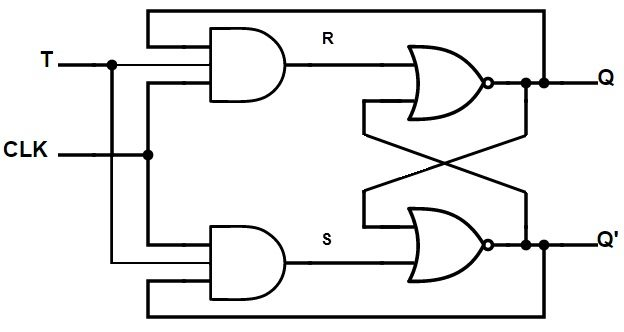
4️⃣ T Flip-Flop​

  • Toggles output on each clock
  • Used in counters

⏱️ Clock: The Heartbeat of Sequential Logic​

Sequential circuits need a clock signal.

  • The clock is a square wave
  • Flip-flops update only on clock edges
  • This makes behavior predictable and synchronized Example:
  • Clock = 1 MHz → 1 million updates per second

Without a clock, complex systems become chaotic.

📦 Building Bigger Systems from Flip-Flops​

Registers​

  • Group of flip-flops
  • Store multi-bit values (8-bit, 16-bit, 32-bit)

Example:

  • CPU registers
  • Configuration registers

Counters​

  • Count up or down on each clock
  • Built from T or JK flip-flops

Used in:

  • Timers
  • Clocks
  • Event counting

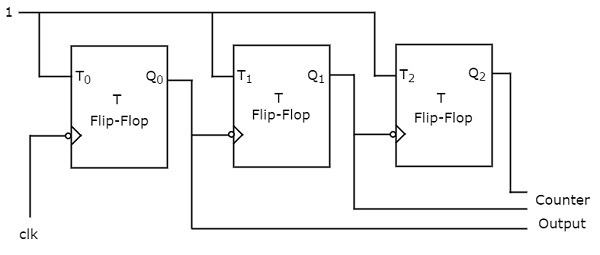
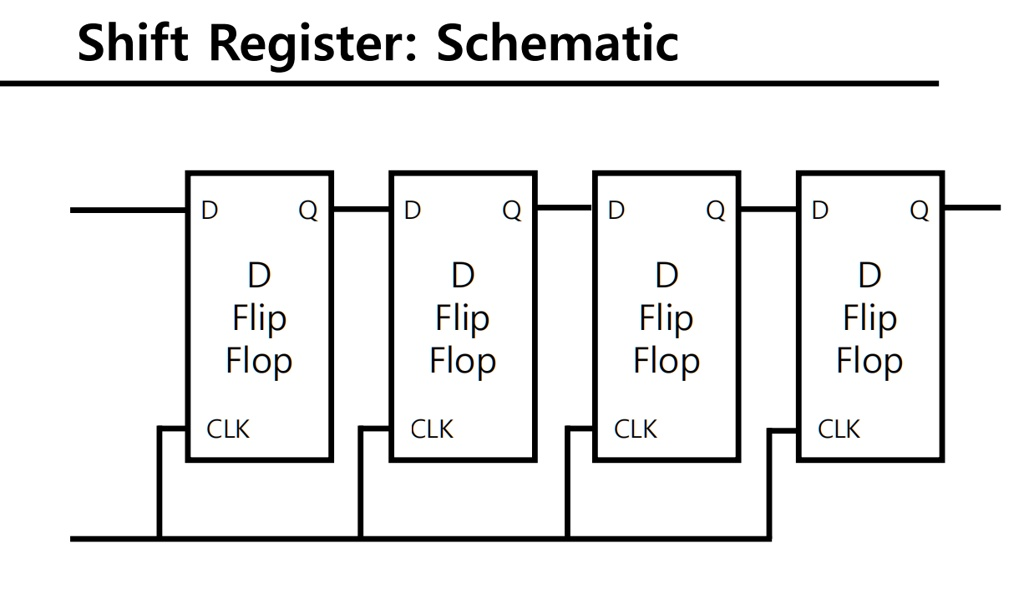
Shift Registers​

  • Move data left or right
  • Used for:
    • Serial communication
    • Data buffering
    • LED animations

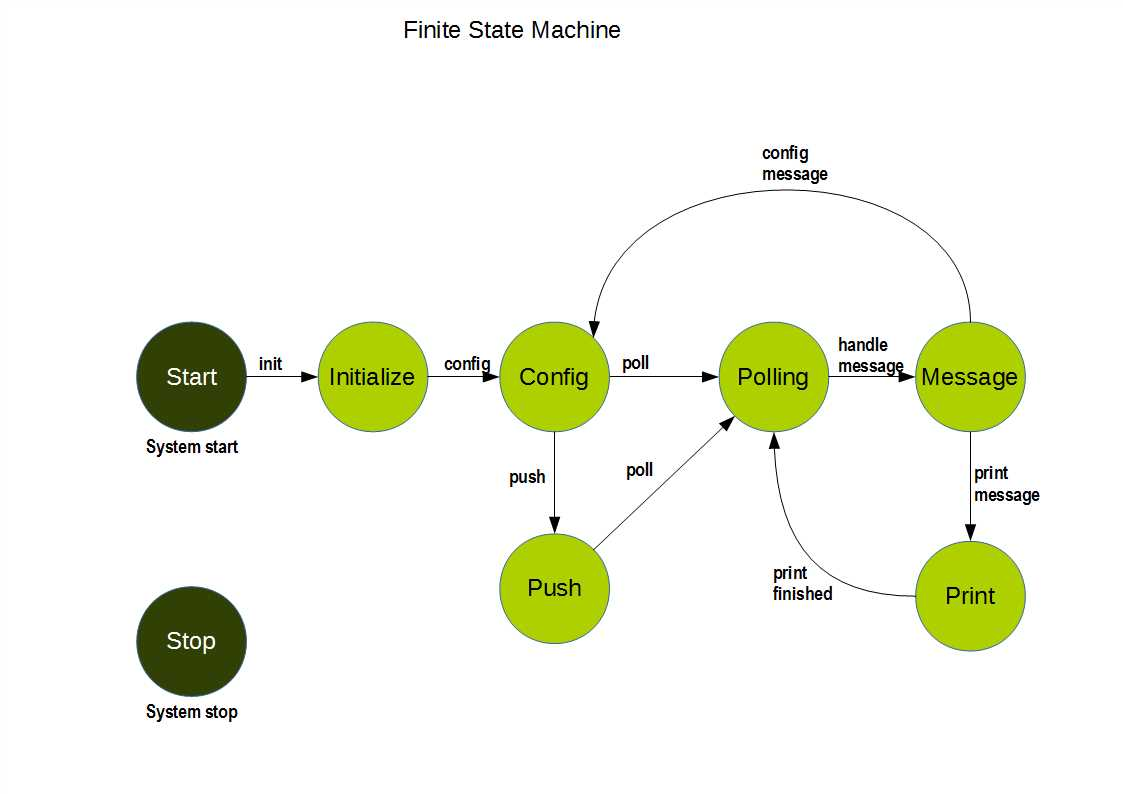
Finite State Machines (FSMs)​

A state machine:

  • Has defined states
  • Moves between states based on inputs and clock

Used in:

  • Traffic lights
  • Communication protocols
  • Motor controllers
  • CPUs

🧩 Combinational + Sequential = Real Systems​

Real digital systems combine both:

Inputs → Combinational Logic → Flip-Flops → Outputs  
↑ |  
└──── Feedback ─┘
  • Combinational logic decides what should happen
  • Flip-flops remember what has happened

🖥️ Example: Simple Counter​

  • Flip-flops store count
  • Combinational logic computes next value
  • Clock updates count

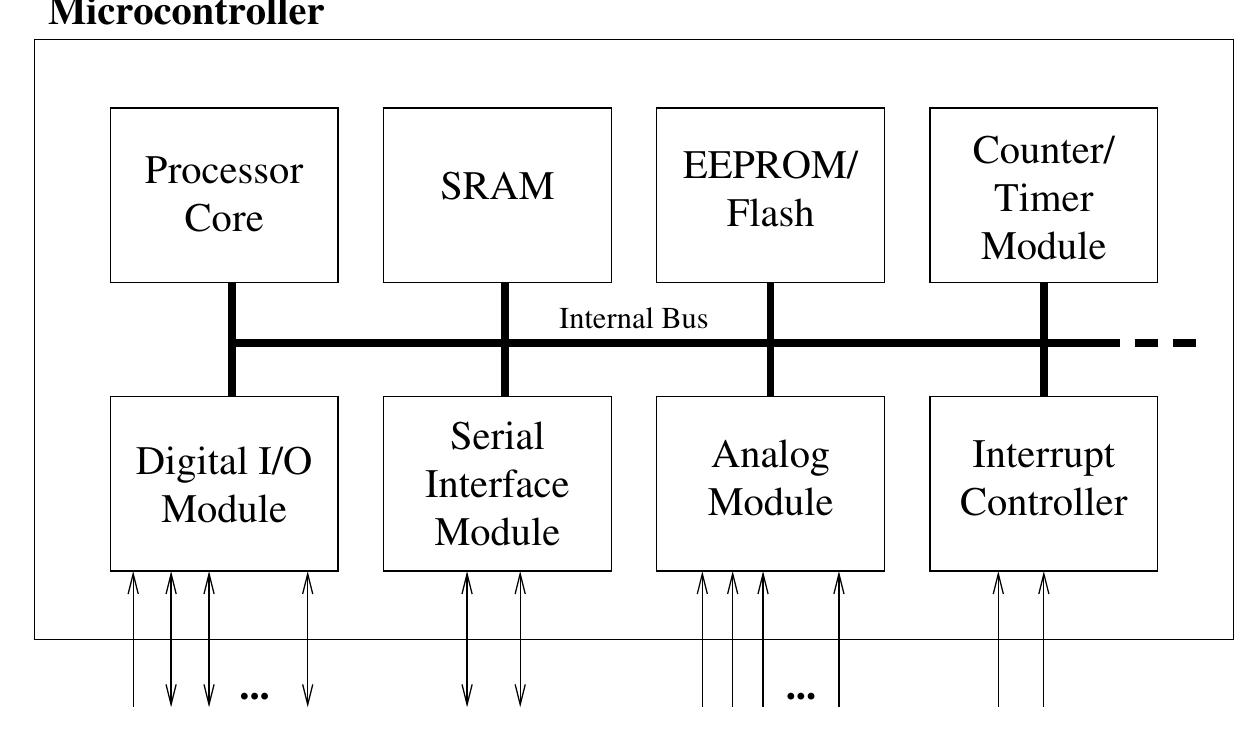
This simple idea scales up to:

  • Microcontrollers
  • Processors
  • RAM
  • GPUs

⚠️ Common Beginner Confusions​

  • Thinking logic gates alone can store data ❌
  • Forgetting clock timing
  • Mixing asynchronous and synchronous logic
  • Ignoring propagation delays
  • Forgetting reset logic

✅ Why This Topic Is CRITICAL​

If you understand:

  • Combinational circuits
  • Sequential circuits
  • Flip-flops
  • Clocks

Then you understand:

  • How CPUs work
  • How memory works
  • How programs execute
  • How digital control systems operate

🏁 The Bottom Line​

  • Combinational circuits compute
  • Sequential circuits remember
  • Flip-flops store bits
  • Clocks synchronize everything
  • Combining them creates computers

Logic gates make decisions
Memory gives them intelligence

This is where electronics stops being simple logic and becomes real computing.