🎛️ Active Filters: Shaping Signals with Precision

In the Fundamentals section, we learned about passive RC filters. They work, but they have limitations:

• Loading effects (output impedance changes frequency response)
• No gain (only attenuation)
• Limited sharpness (gentle roll-off)

Active filters solve all these problems using op-amps.

---

🔍 Why Active Filters?

Feature	Passive Filter	Active Filter
Gain	Always < 1	Can be > 1
Loading	Sensitive to load	Buffered output
Roll-off	20dB/decade max	Can be steeper
Tuning	Hard (component interaction)	Easier (independent controls)
Size	Large inductors needed for LF	No inductors!
Cost	Low	Moderate

---

🎯 Filter Basics Refresher

What Filters Do

• Pass certain frequencies
• Reject (attenuate) others

Four Basic Types

1. Low-Pass Filter (LPF): Passes low frequencies, blocks high frequencies
2. High-Pass Filter (HPF): Passes high frequencies, blocks low frequencies
3. Band-Pass Filter (BPF): Passes a band of frequencies
4. Band-Stop Filter (BSF): Blocks a band of frequencies (notch filter)

---

📊 Key Filter Parameters

Cutoff Frequency ($f_c$)

The frequency where output is -3dB (0.707× or 70.7%) of passband value.

Roll-off Rate

How quickly the filter attenuates outside the passband.

• 1st order: 20dB/decade
• 2nd order: 40dB/decade
• 3rd order: 60dB/decade

Quality Factor (Q)

Determines the sharpness of the response (important for band-pass filters).

---

📉 First-Order Low-Pass Filter

The Circuit

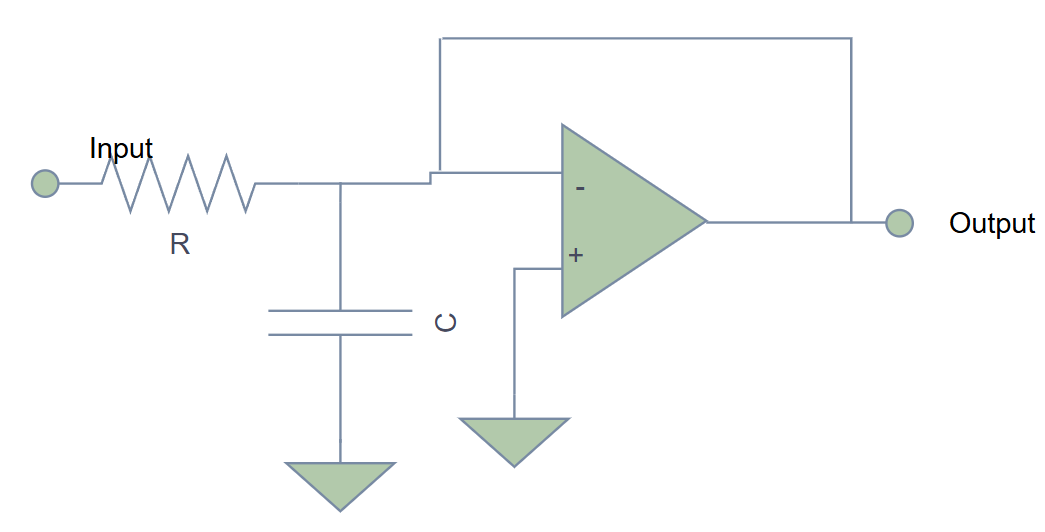
The Math

Cutoff frequency:

$$f_c = \frac{1}{2\pi RC}$$

Gain at DC: Set by resistor divider (typically 1 for unity-gain)

Frequency response:

$$|H(f)| = \frac{A_v}{\sqrt{1 + (f/f_c)^2}}$$

At $f = f_c$: Output is 0.707× input (−3dB)

Roll-off: 20dB/decade above $f_c$

---

🎚️ Design Example: Audio Subwoofer Filter

Goal: Pass frequencies below 200Hz, reject above

Design:

• $f_c = 200Hz$
• Choose $C = 100nF$ (common value)

Calculate $R$:

$$R = \frac{1}{2\pi f_c C} = \frac{1}{2\pi \times 200 \times 100 \times 10^{-9}} = 7.96k\Omega$$

Use standard value: $R = 8.2k\Omega$

Result: Clean bass signal with treble removed!

---

Capacitor Selection

For audio filters:

• Film capacitors (polypropylene): Best for audio quality
• Ceramic capacitors (X7R/C0G): Good for general use, cheaper
• Avoid electrolytics in signal path (use for power supply filtering only)

---

📈 First-Order High-Pass Filter

The Circuit

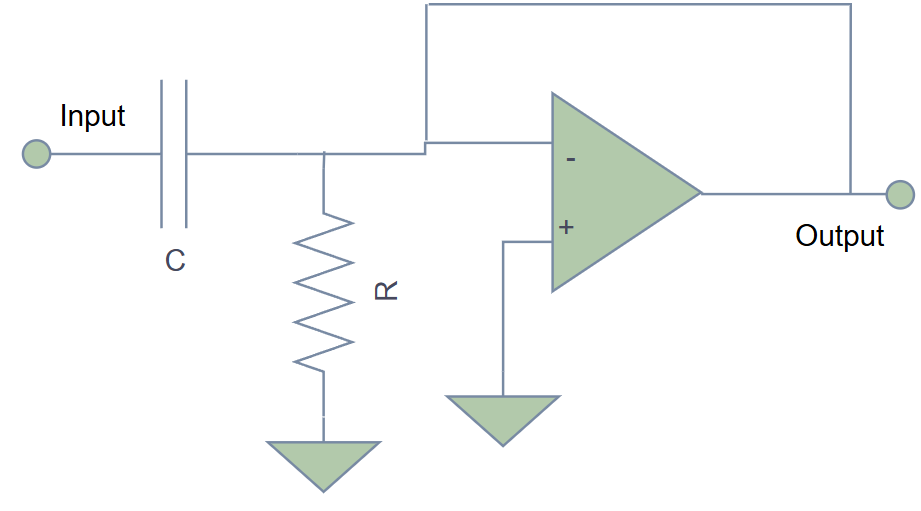
The Math

Cutoff frequency:

$$f_c = \frac{1}{2\pi RC}$$

Frequency response:

$$|H(f)| = \frac{A_v \cdot (f/f_c)}{\sqrt{1 + (f/f_c)^2}}$$

At $f = f_c$: Output is 0.707× input (−3dB)

Roll-off: 20dB/decade below $f_c$

---

🎤 Design Example: Microphone AC Coupling

Goal: Remove DC offset, pass audio (20Hz and above)

Design:

• $f_c = 20Hz$
• Choose $R = 100k\Omega$ (high impedance for low noise)

Calculate $C$:

$$C = \frac{1}{2\pi f_c R} = \frac{1}{2\pi \times 20 \times 100k} = 79.6nF$$

Use standard value: $C = 82nF$ or $100nF$

Result: DC blocked, audio passes cleanly!

---

🎯 Second-Order Filters: Steeper is Better

First-order filters are gentle. For sharper filtering, we need second-order (or higher).

Advantages

• 40dB/decade roll-off (twice as steep)
• Better separation between pass and stop bands
• More design control

Popular Topologies

1. Sallen-Key (voltage-controlled)
2. Multiple Feedback (MFB)
3. State Variable (versatile but complex)

We'll focus on Sallen-Key (most common).

---

📉 Second-Order Low-Pass Filter (Sallen-Key)

The Circuit

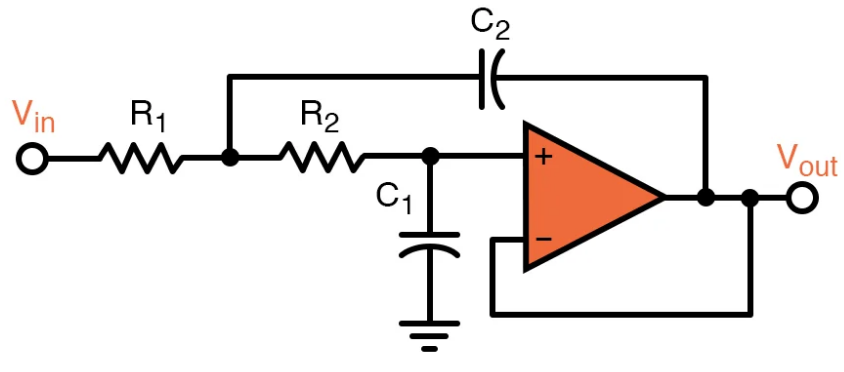
Design Equations

For Butterworth response (maximally flat):

Equal component values:

• $R_1 = R_2 = R$
• $C_1 = C_2 = C$

Cutoff frequency:

$$f_c = \frac{1}{2\pi RC}$$

Op-amp gain: $A_v = 1.586$ (for Butterworth)

Set using: $A_v = 1 + \frac{R_f}{R_g}$

---

🔊 Design Example: Anti-Aliasing Filter

ADC sampling: 10kHz
Anti-aliasing filter: $f_c = 4kHz$ (Nyquist = 5kHz)

Design:

• Choose $C = 10nF$
• Calculate: $R = \frac{1}{2\pi \times 4000 \times 10 \times 10^{-9}} = 3.98k\Omega$
• Use $R = 3.9k\Omega$
• Set gain: $A_v = 1.586$ using $R_f = 5.86k\Omega$, $R_g = 10k\Omega$

Result: Sharp cutoff prevents aliasing, signal integrity maintained!

---

Filter Response Types

Different applications need different responses:

Type	Characteristic	Use Case
Butterworth	Maximally flat passband	General purpose
Chebyshev	Steeper roll-off, ripple in passband	When sharp cutoff needed
Bessel	Linear phase (no distortion)	Audio, data transmission

---

📈 Second-Order High-Pass Filter (Sallen-Key)

The Circuit

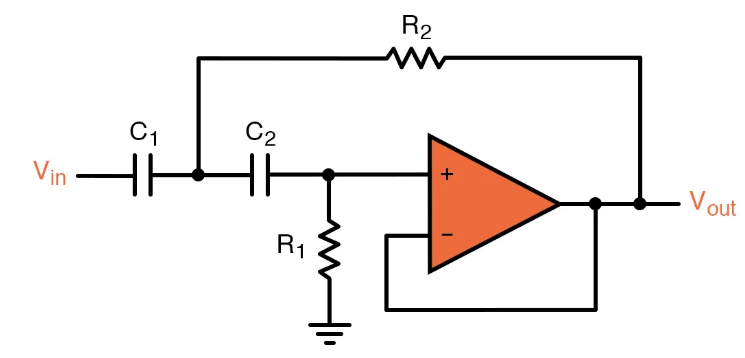
Design Equations

For Butterworth:

• $C_1 = C_2 = C$
• $R_1 = R_2 = R$

Cutoff frequency:

$$f_c = \frac{1}{2\pi RC}$$

Op-amp gain: $A_v = 1.586$

---

📡 Design Example: Infrasonic Filter for Audio

Goal: Remove rumble and handling noise below 20Hz

Design:

• $f_c = 20Hz$
• Choose $C = 1\mu F$ (larger C for low frequency)
• Calculate: $R = \frac{1}{2\pi \times 20 \times 1 \times 10^{-6}} = 7.96k\Omega$
• Use $R = 8.2k\Omega$
• Set gain: $A_v = 1.586$

Result: Clean audio, no low-frequency rumble!

---

🎵 Band-Pass Filter

Combines high-pass and low-pass.

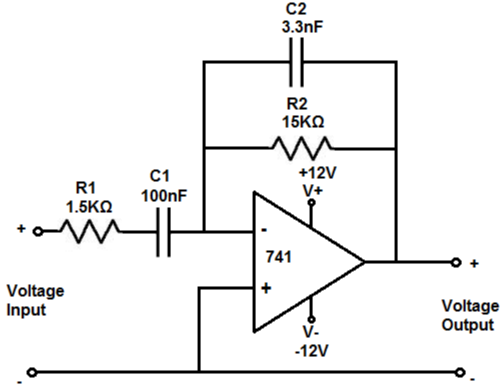
Two Approaches

1. Cascade (Simple)

HPF → LPF in series

Requirements: $f_{c(HP)} < f_{c(LP)}$

Bandwidth: $BW = f_{c(LP)} - f_{c(HP)}$

2. Dedicated Band-Pass (MFB)

Single op-amp, optimized for narrow bands.

---

📻 Design Example: Voice Band Filter (300Hz - 3kHz)

Cascade approach:

HPF stage:

• $f_c = 300Hz$
• $C = 100nF$, $R = 5.3k\Omega$

LPF stage:

• $f_c = 3kHz$
• $C = 10nF$, $R = 5.3k\Omega$

Bandwidth: $3kHz - 300Hz = 2.7kHz$

Result: Perfect for voice communication, rejects noise outside speech range!

---

🚫 Band-Stop (Notch) Filter

Used to remove specific unwanted frequencies.

Common Application: 50/60Hz Mains Hum Removal

Twin-T Notch Filter:

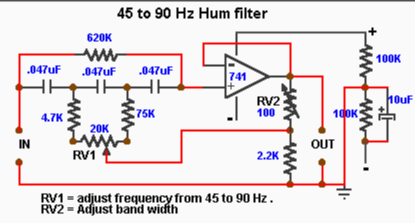
• Two T-networks (RC and CR) in parallel
• Op-amp buffer

Design for 50Hz notch:

• Choose $C = 1\mu F$
• $R = \frac{1}{2\pi f C} = \frac{1}{2\pi \times 50 \times 1 \times 10^{-6}} = 3.18k\Omega$

Result: Removes 50Hz hum while passing everything else!

---

🔬 Filter Design Process

Step-by-Step

1. Define Requirements

   • Passband frequency range
   • Stopband frequency range
   • Attenuation needed
   • Acceptable ripple

2. Choose Filter Type

   • Butterworth (general)
   • Chebyshev (steep roll-off)
   • Bessel (phase linearity)

3. Determine Order

   • 1st order: 20dB/decade
   • 2nd order: 40dB/decade
   • 3rd order: 60dB/decade

4. Select Topology

   • Sallen-Key (most common)
   • MFB (inverting, good CMRR)
   • State variable (adjustable)

5. Calculate Components

   • Use design equations
   • Select standard values
   • Verify cutoff frequency

6. Set Op-Amp Gain

   • Butterworth: 1.586
   • Unity gain: simpler but less sharp

7. Simulate & Test

---

⚡ Practical Design Tips

Resistor Selection

• Use 1% tolerance or better
• Typical range: 1kΩ to 100kΩ
• Avoid very high values (noise)
• Avoid very low values (loading)

Capacitor Selection

• Use film caps for precision
• C0G/NP0 ceramics for stability
• Typical range: 10pF to 1µF
• Match capacitors in pairs if possible

Op-Amp Selection

• Low noise: OPAx134, LT1028
• High speed: OPA684, AD8099
• General purpose: TL07x, LM358
• Precision: OPA2277, AD8628

Power Supply

• Use ±15V or ±12V for maximum headroom
• Single supply: Add DC offset (V/2)
• Decouple op-amp power pins

---

📊 Common Design Pitfalls

Problem	Cause	Solution
Oscillation	Insufficient phase margin	Add small capacitor across feedback resistor
Noise	Poor grounding, layout	Star grounding, short traces
Distortion	Op-amp slew rate too low	Choose faster op-amp
DC offset drift	Temperature, bias current	Use precision op-amp or AC coupling
Wrong cutoff	Component tolerance	Measure and adjust, use trimmers

---

🧪 Lab Exercise: Build a Tone Control

Objective: Create bass/treble control for audio

Circuit:

• Bass: 2nd-order LPF, adjustable cutoff (50-200Hz)
• Treble: 2nd-order HPF, adjustable cutoff (5kHz-20kHz)
• Summing amplifier: Combine bass + mid + treble

Components:

• Op-amps: TL072 (dual)
• Potentiometers for cutoff adjustment
• Film capacitors
• 1% resistors

Test:

• Apply music signal
• Observe frequency response on oscilloscope
• Measure cutoff frequencies
• Adjust for desired tone

---

✅ Key Takeaways

• Active filters use op-amps for gain and buffering
• 1st order: 20dB/decade, simple but gentle
• 2nd order: 40dB/decade, sharper transitions
• Sallen-Key is the most common topology
• Butterworth gives flat passband response
• Component selection greatly affects performance
• Higher-order filters = cascading 2nd-order sections

---

🎓 Looking Ahead

Active filters are essential for:

• Data acquisition (anti-aliasing)
• Audio processing (equalizers, crossovers)
• Communications (channel selection)
• Control systems (noise rejection)
• Instrumentation (signal conditioning)

Next, we'll explore instrumentation amplifiers which often include built-in filtering!

---

📚 Further Resources

• Calculate filter designs: Online filter calculators (e.g., Analog Devices Filter Wizard)
• Simulate circuits: LTSpice, TINA-TI
• Study filter response: Plot magnitude and phase
• Experiment with different topologies and orders